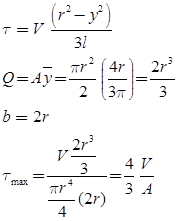Bending Stress In A Circular Beam

In a member of constant cross section the maximum bending moment will govern the design of the section size when we know what kind of normal stress is caused by it.

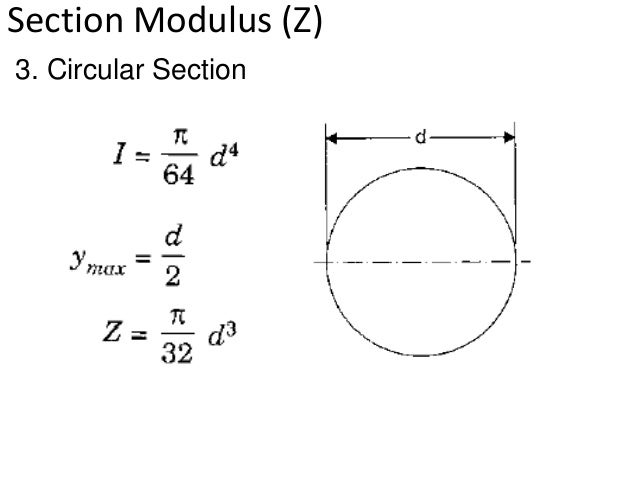
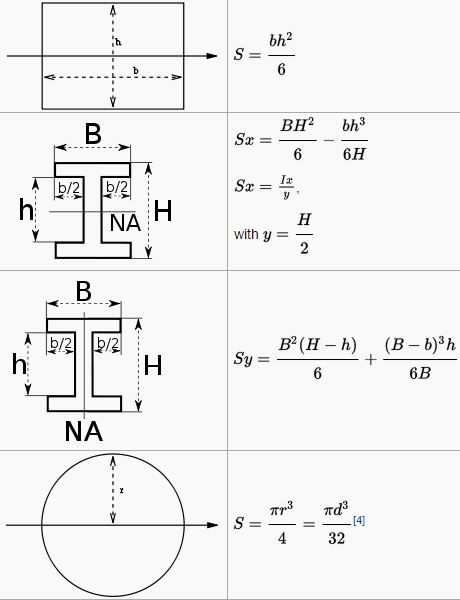
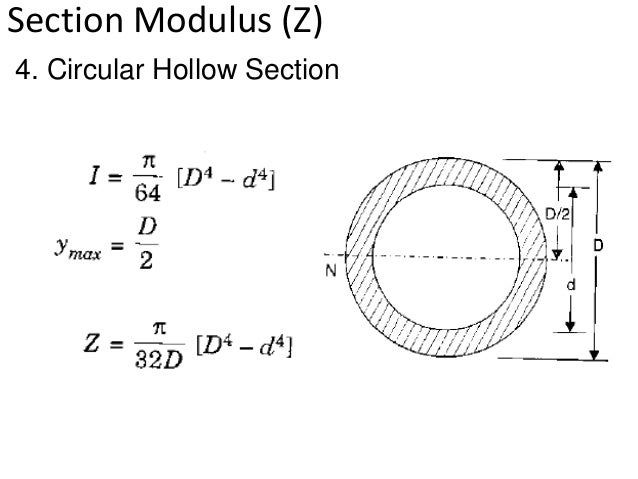
Bending stress in a circular beam. Equation 5 43 applies with equal rigor to circular tubes since the same assumptions stated in the foregoing are valid. One is called a simply supported structural beam bending and the other is called cantilever bending. When the resultant acts away from the shear centre axis then the beam will not only bend but also twist. The general formula for bending or normal stress on the section is given by.

Hollow circular cross section fig. For every calculated normal stress there is a corresponding induced shear stress. σ x m z y i z m z w z displaystyle sigma x frac m z y i z frac m z w z where. The value of the shear stress is equal to half that of the normal stress.

The bending stress is zero at the beam s neutral axis which is coincident with the centroid of the beam s cross section. 3 5 4 longitudinal strains in beams consider a portion ab of a beam in pure bending produced by a positive bending moment m the cross section may be of any shape provided it is symmetric about y axis under the moment m its axis is bent into a circular curve cross section mn and pq remain plane and normal to longitudinal lines plane remains plane can be established by experimental result. When a beam is transversely loaded in such a manner that the resultant force passes through the longitudinal shear centre axis the beam only bends and no torsion will occur. Comment this result shows that the largest shear stress in a circular beam is 4 3 times the average shear stress τ avg v a.

The classic formula for determining the bending stress in a beam under simple bending is. Bending stress or flexural stress commonly occurs in two instances shown in figure 1 5. Combined stress circular cantilever beam in direct compression and bending stress equations and calculator circular cantilever beam in direct compression. In both cases the stress normal for bending and shear for torsion is equal to a couple moment m for bending and t for torsion times the location along the cross section because the stress isn t uniform along the cross section with cartesian coordinates for bending and cylindrical coordinates for torsion all divided by the second moment of area of the cross section.

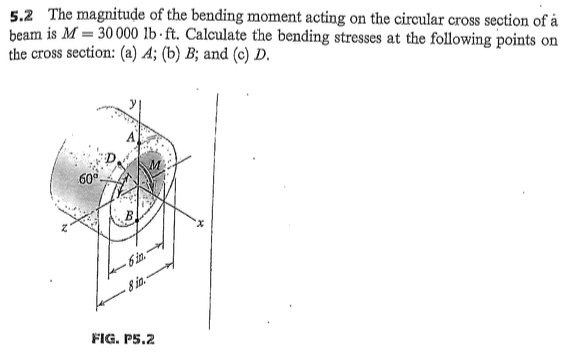
For internal equilibrium to be maintained the bending moment will be equal to the m from the normal stresses the areas the moment arms. Thus the maximum bending stress will occur either at the top or the bottom of the beam section depending on which distance is larger.